|
|
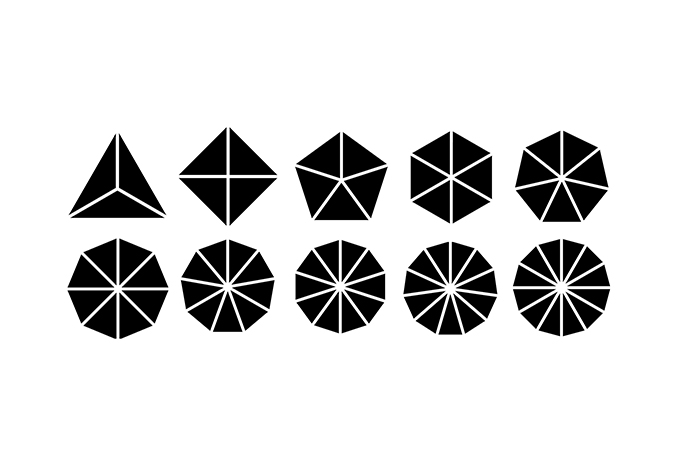
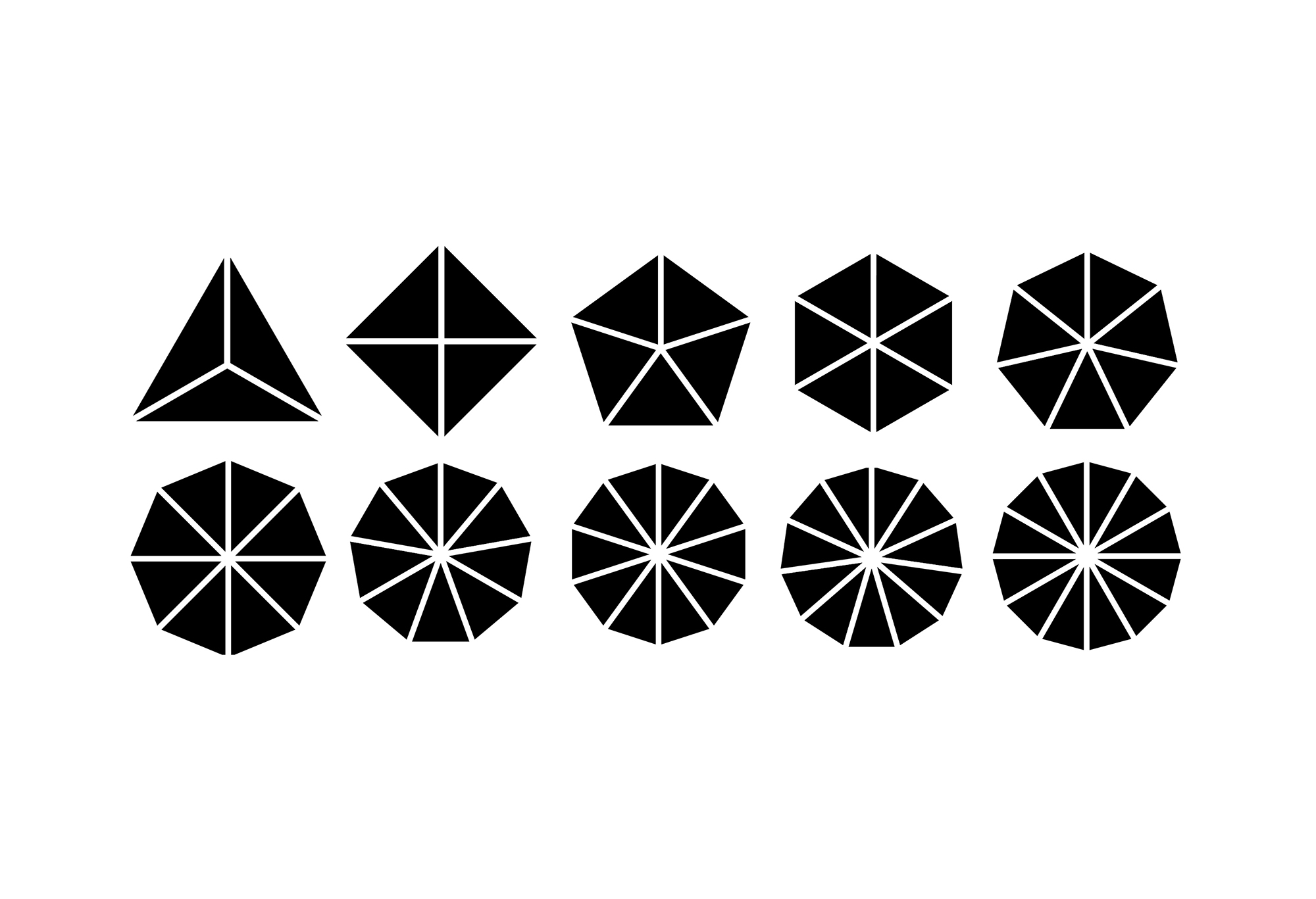
01. Divisions of regular n-gons, for n ≤ 12.
|
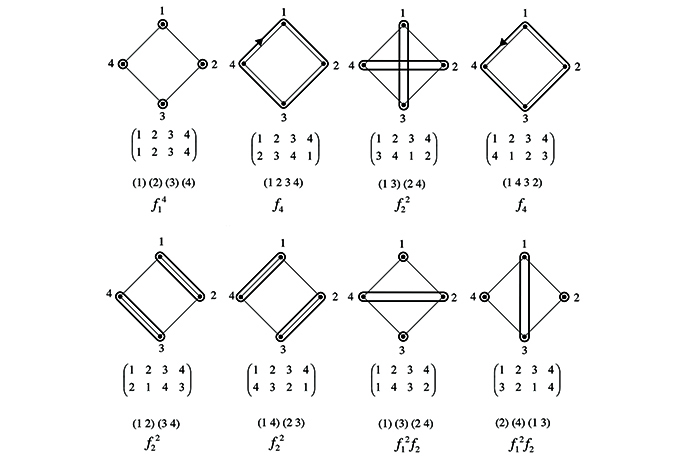
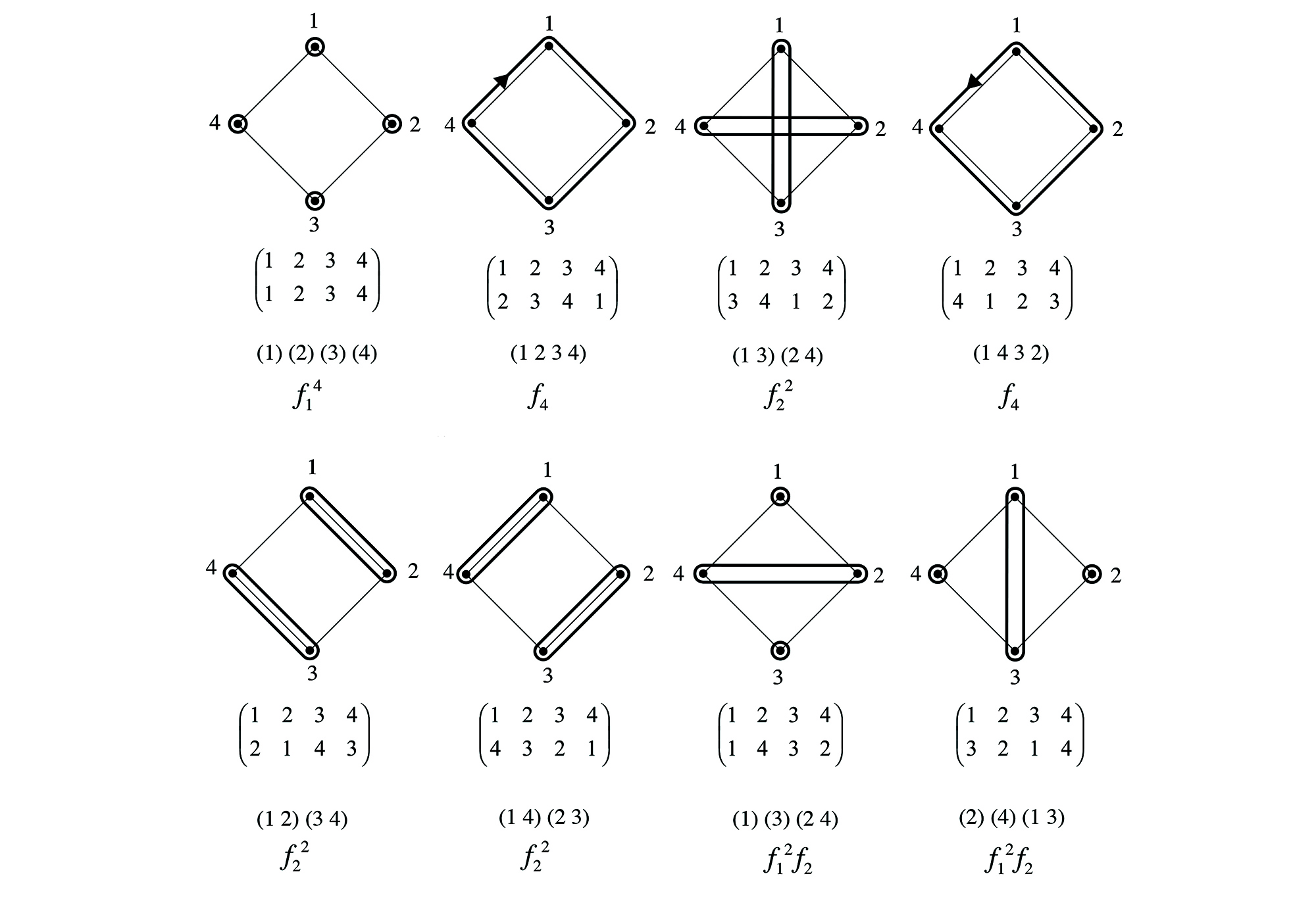
02. Cycle index of permutation group of vertices of an n-gon, here, n = 4
|
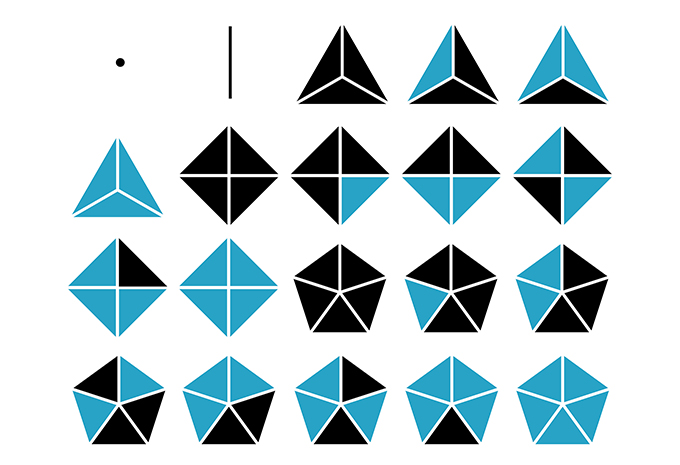
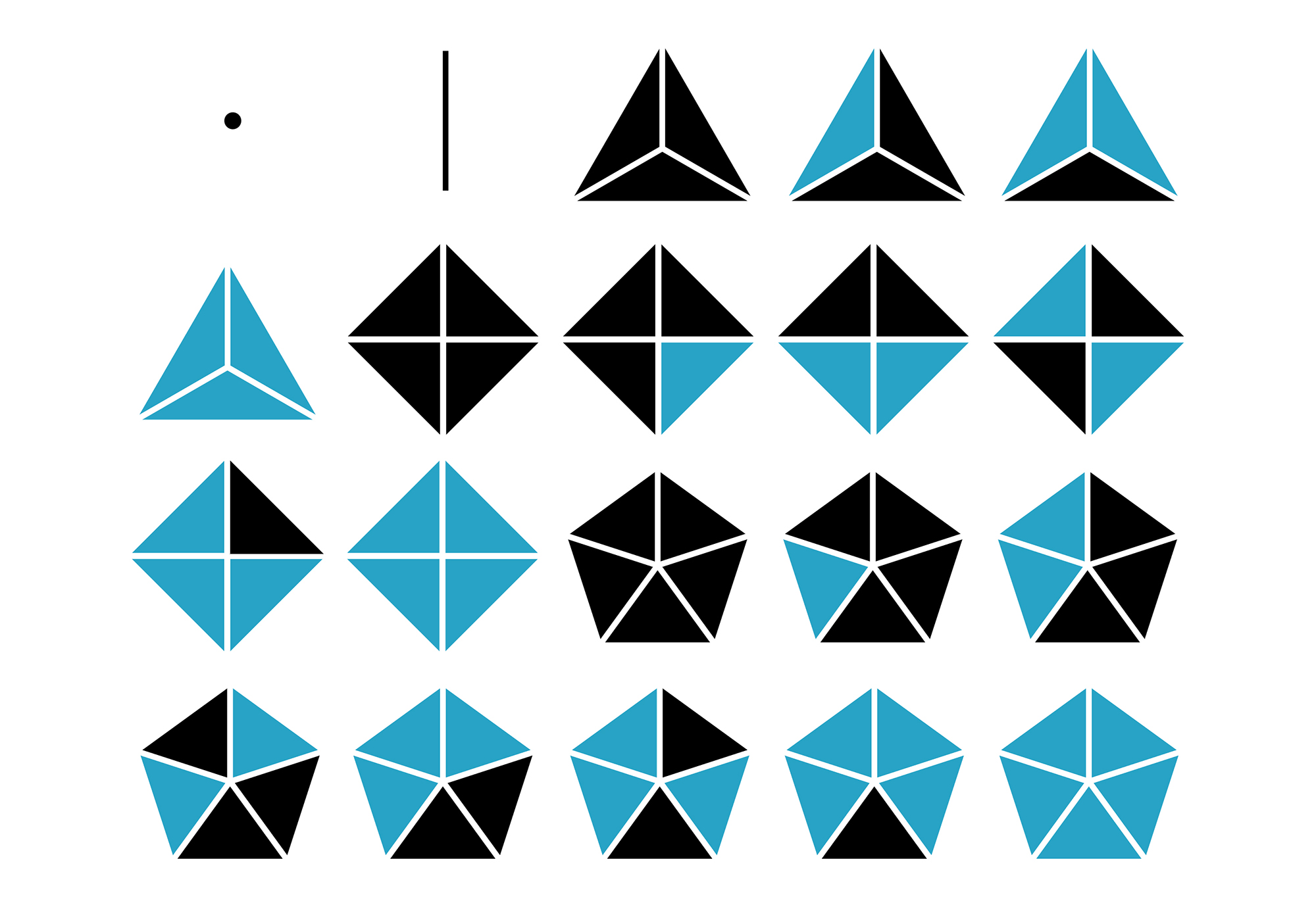
03. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (1-20)
|


04. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (21-40)
|


05. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (41-60)
|


06. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (61-80)
|


07. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (81-100) |


08. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (101-120)
|


09. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (121-140)
|


10.A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (141-160)
|


11. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (161-180)
|


11. A visual enumeration of the 555 non-equivalent configurations of two-coloring configurations of regular n-gons, for n ≤ 12: (181-200)
|
|
The sieve is a powerful formal tool developed by Xenakis to create integer-sequence generators that can be used for the generation of various numerical patterns to represent pitch scales, rhythm sequences, as well as patterns of loudness, density, timber and so forth (1). Xenakis used the sieves in a series of musical and architectural works (2), (3), (4)
The key motivation for the work outlined here is to capture and visualize the properties of the algebra of the sieves looking at the decomposition of the moduli that emerge out of the combination of the sieves. Xenakis asserted that his algebra of sieves revealed insights into fundamental aspects of composition. Here these hidden symmetries are identified and foregrounded for any modulus however complex.
The formal tools for the inquiry on sieves are taken from Lagrange’s theorem on subgroups of given order and Polya’s theorem of counting non-equivalent configurations with respect to a given permutation group. Here the theorems are applied within an automated computational framework that automatically generates all the symmetry subgroups of a given symmetry group (5), calculates the cyclic index of all symmetry groups and subgroups of any finite shape (6), computes the figure inventory of any number of variables upon the cycle index (7), produces patches showing the data flow of the moduli (8) and visualizes the result of all non-equivalent configurations with corresponding isomorphic two-dimensional subshapes of regular n-gons (9). The project, background, framework and formal details are given in (10).
|
|
|
|