|
|
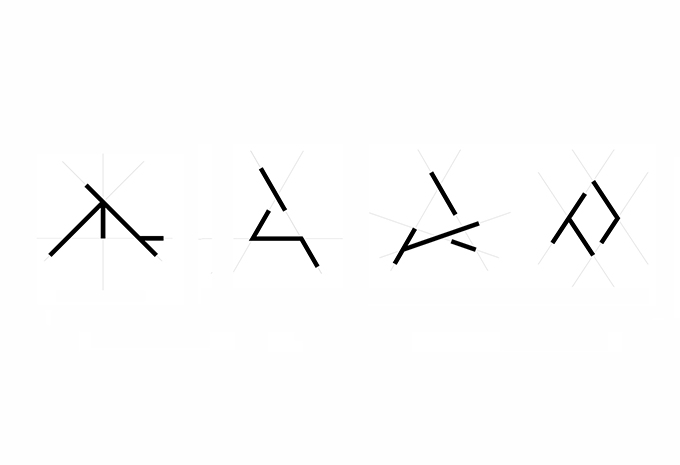
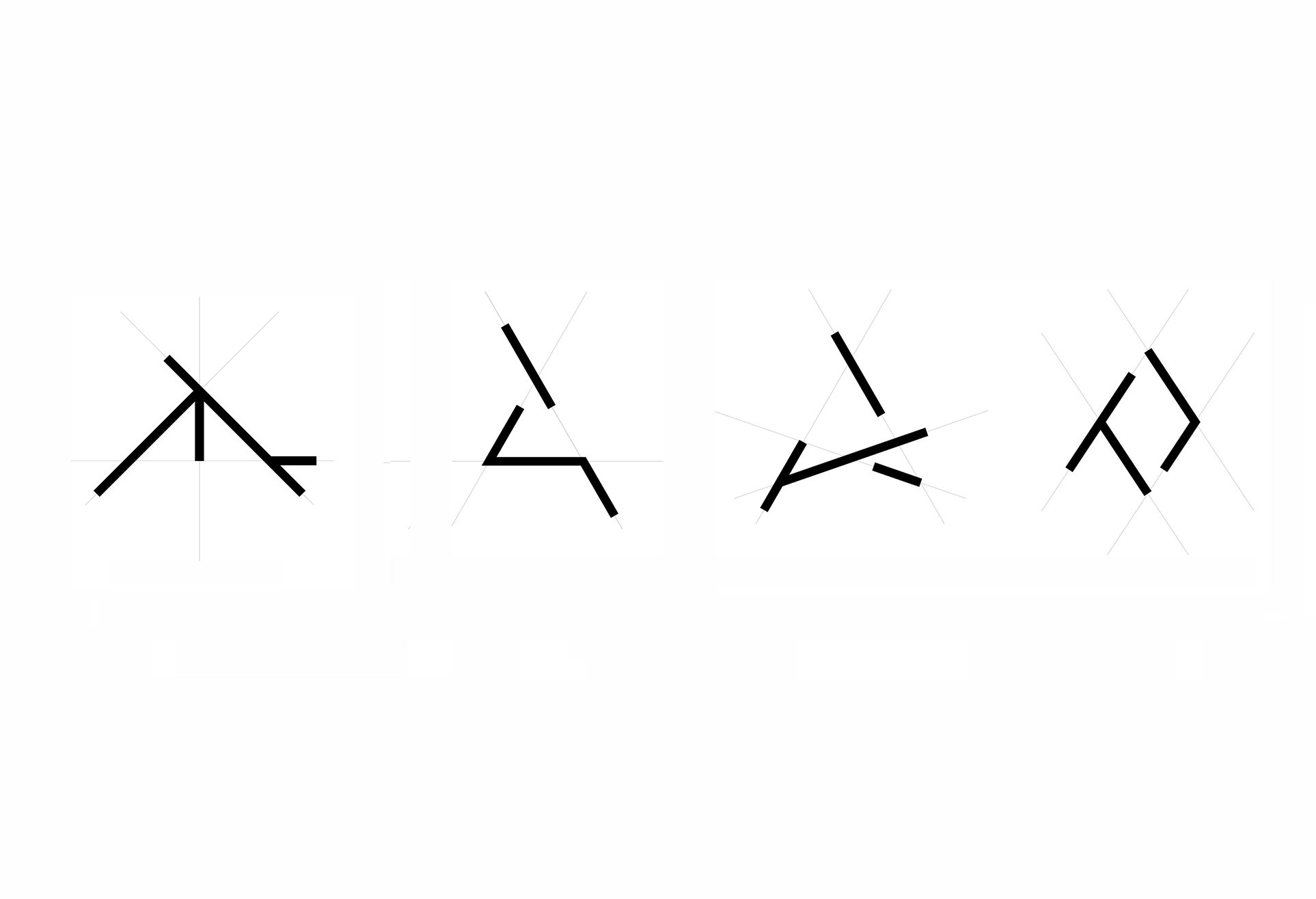
01. Four shapes consisting of 4 lines each
|
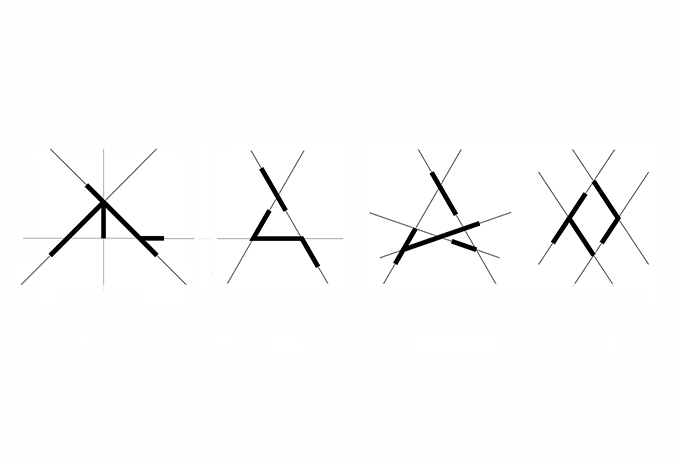
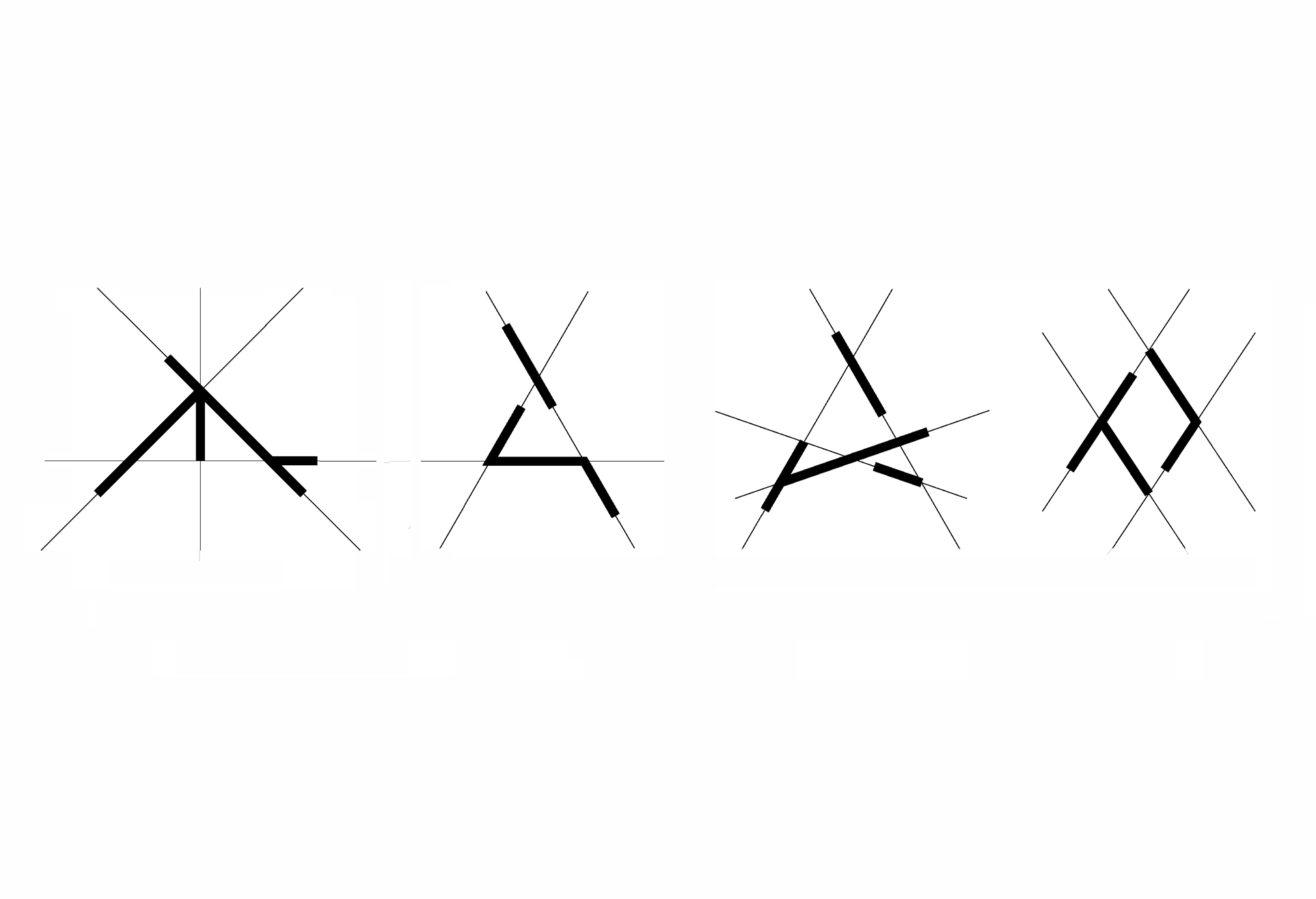
02. Shapes as collections of maximal lines upon construction lines (carrier lines)
|
03. Registration points mark the intersections of two or more construction lines and produce regions in each construction line. (a) No registration point: One region; (b) One registration point: 3 regions in two orientations; (c) Two registration points: 5 regions
|
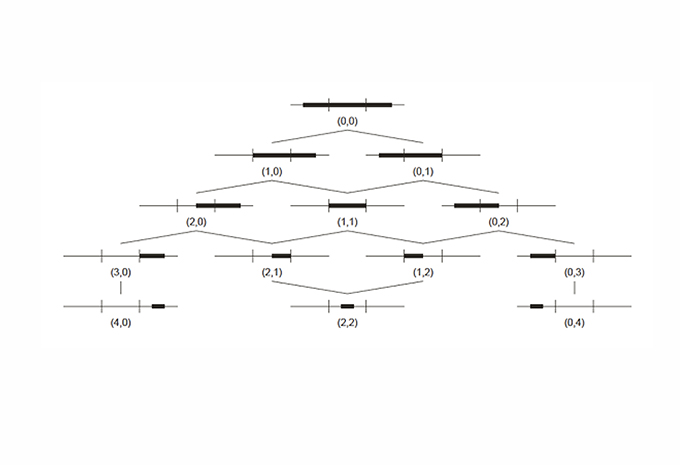
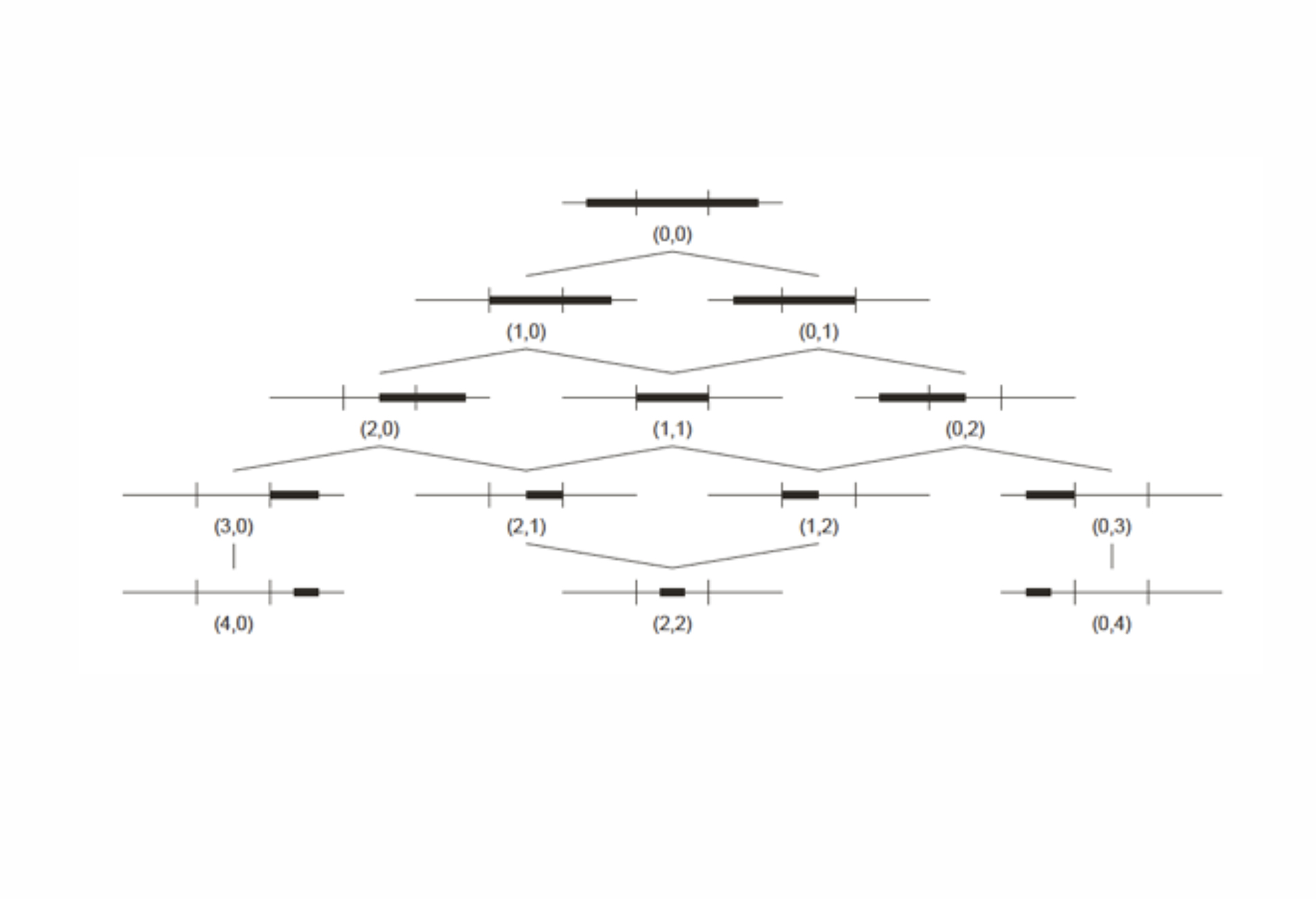
04. Maximal lines are bounded by points in the regions defined by the registration points. The 13 ways of placing lines in a construction with 2 registration points can be ordered in a partial order set by inclusion
|
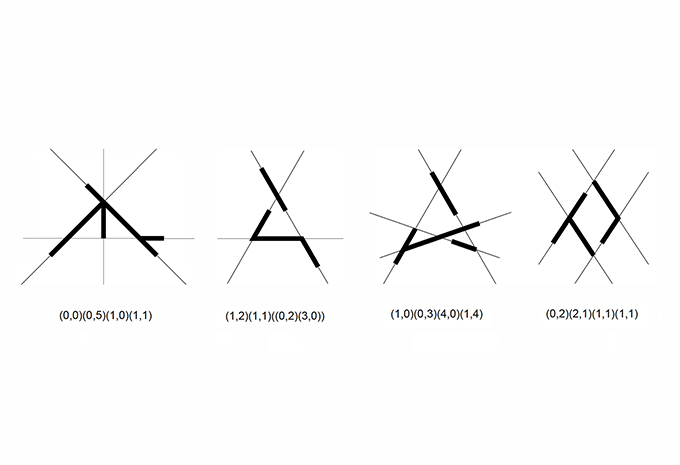
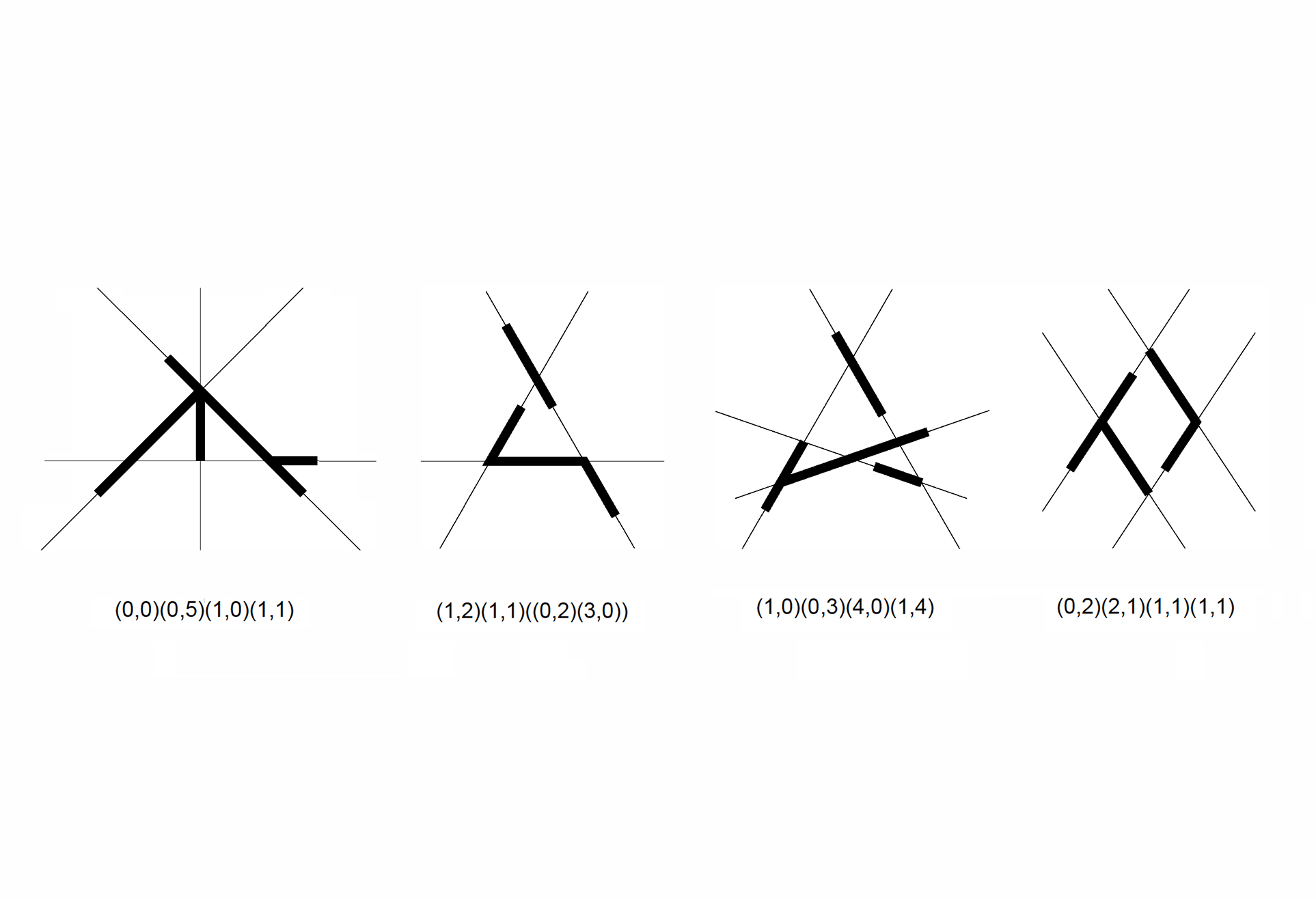
05. The shape signature of a shape is the ordered sequence of pairs of boundary elements embedded in distinct regions of the construction lines
|
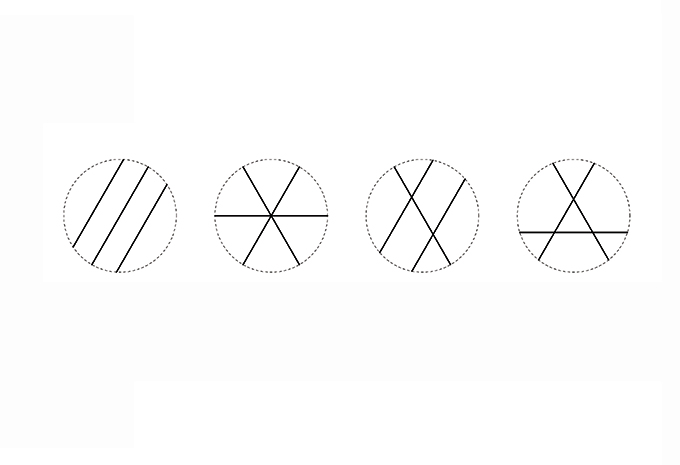
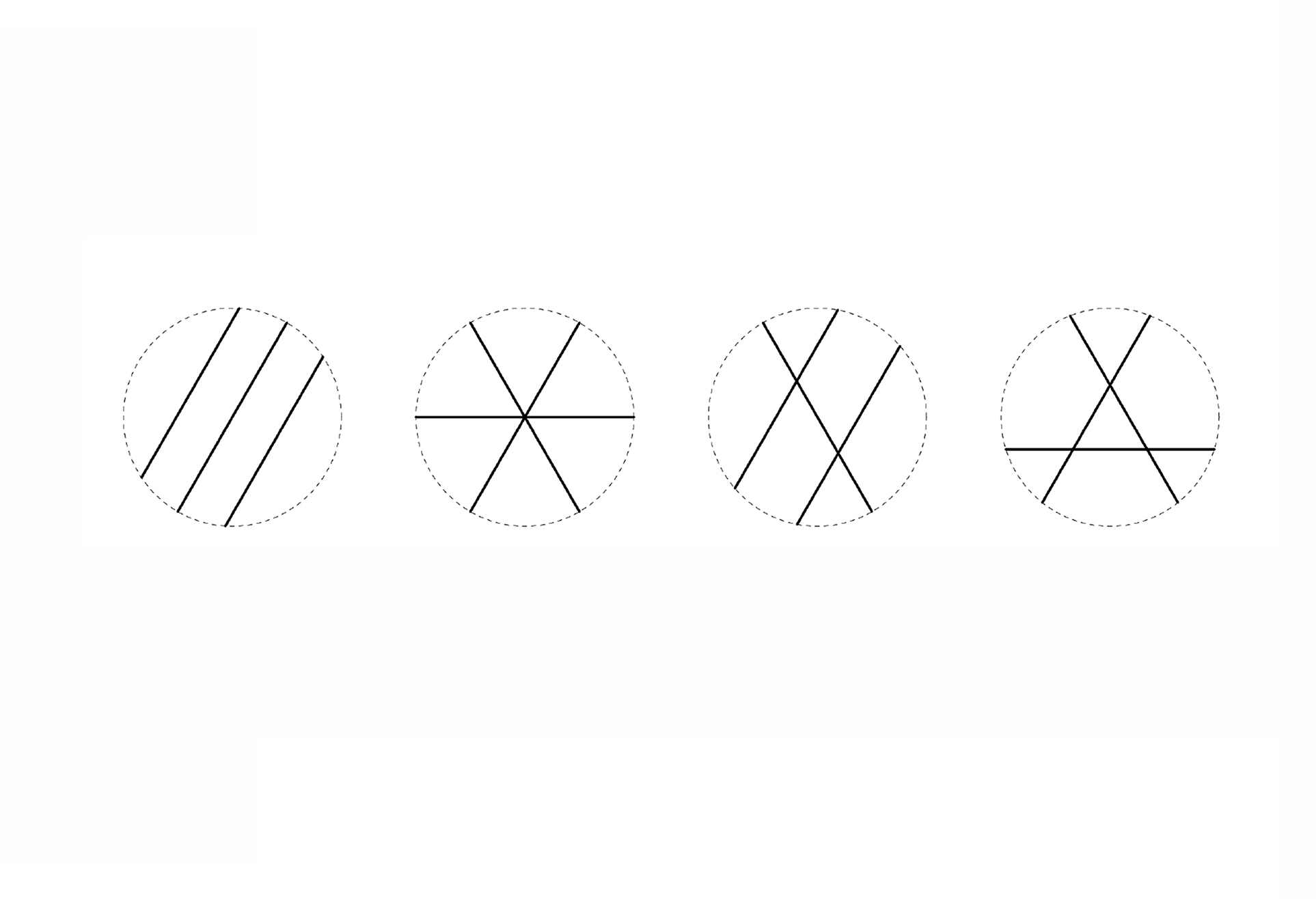
06. Counting shapes: For k construction lines, l registration points and m maximal lines; (a) 3,0,3; (b) 3,1,3; (c) 3,2,3; and (d) 3,3,3. The type of valency of intersection counts too.
|
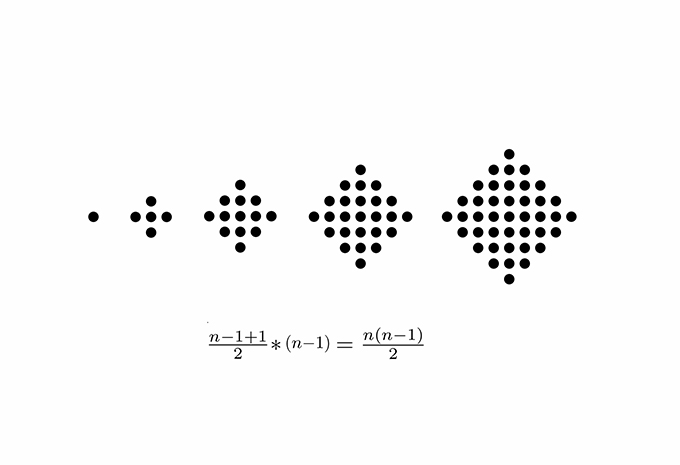

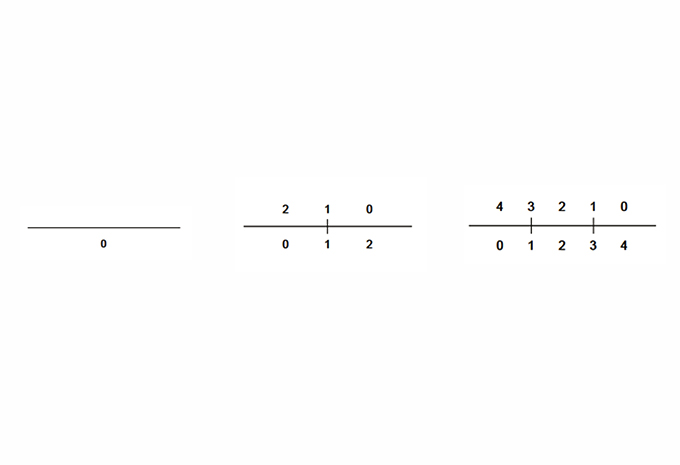
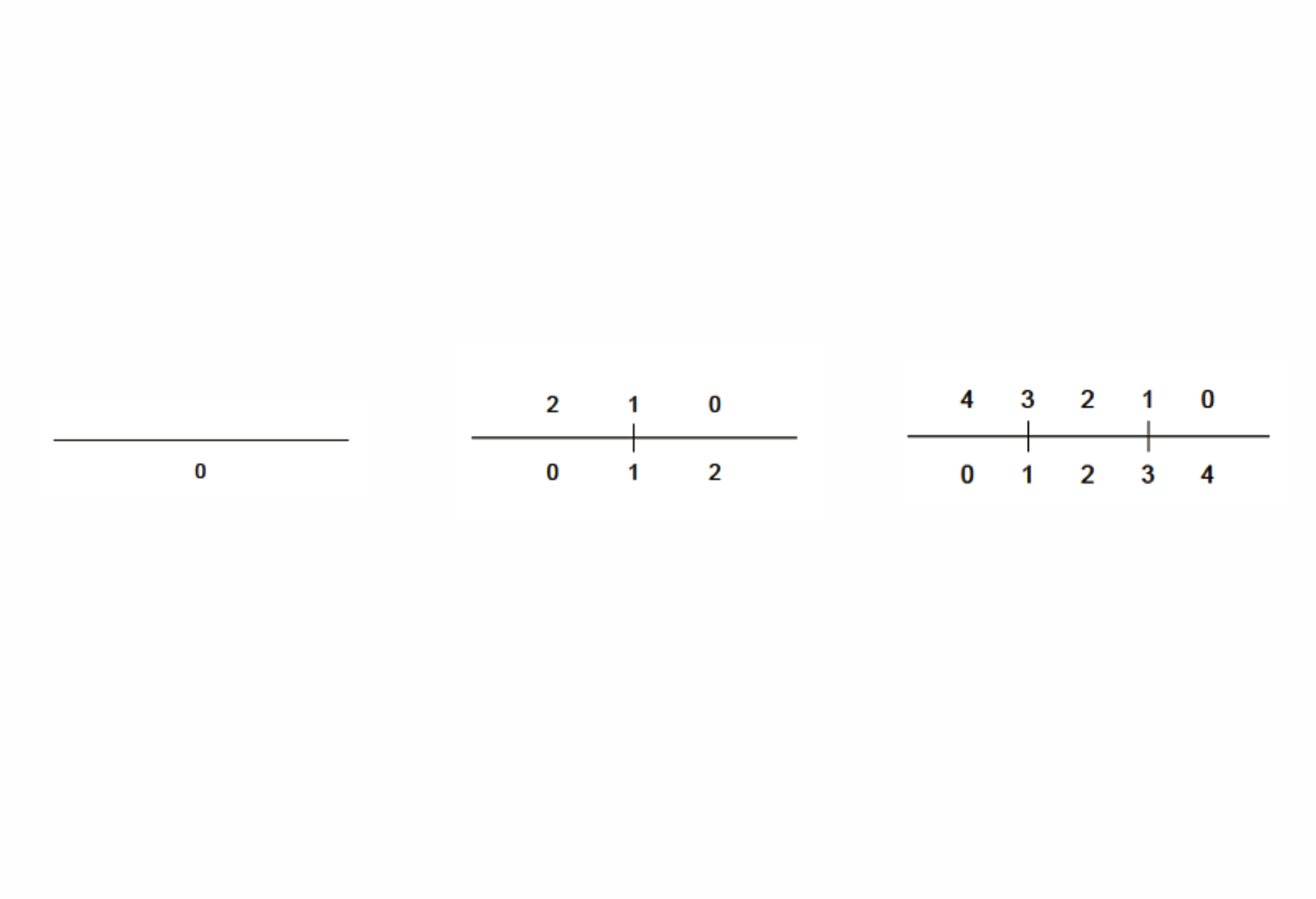
07. The number of ways to place one maximal line on a construction line with k registration points is the sequence of centered square numbers.
|
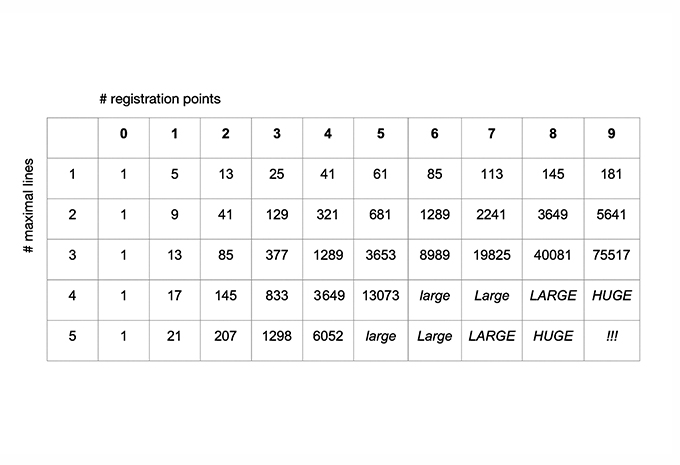
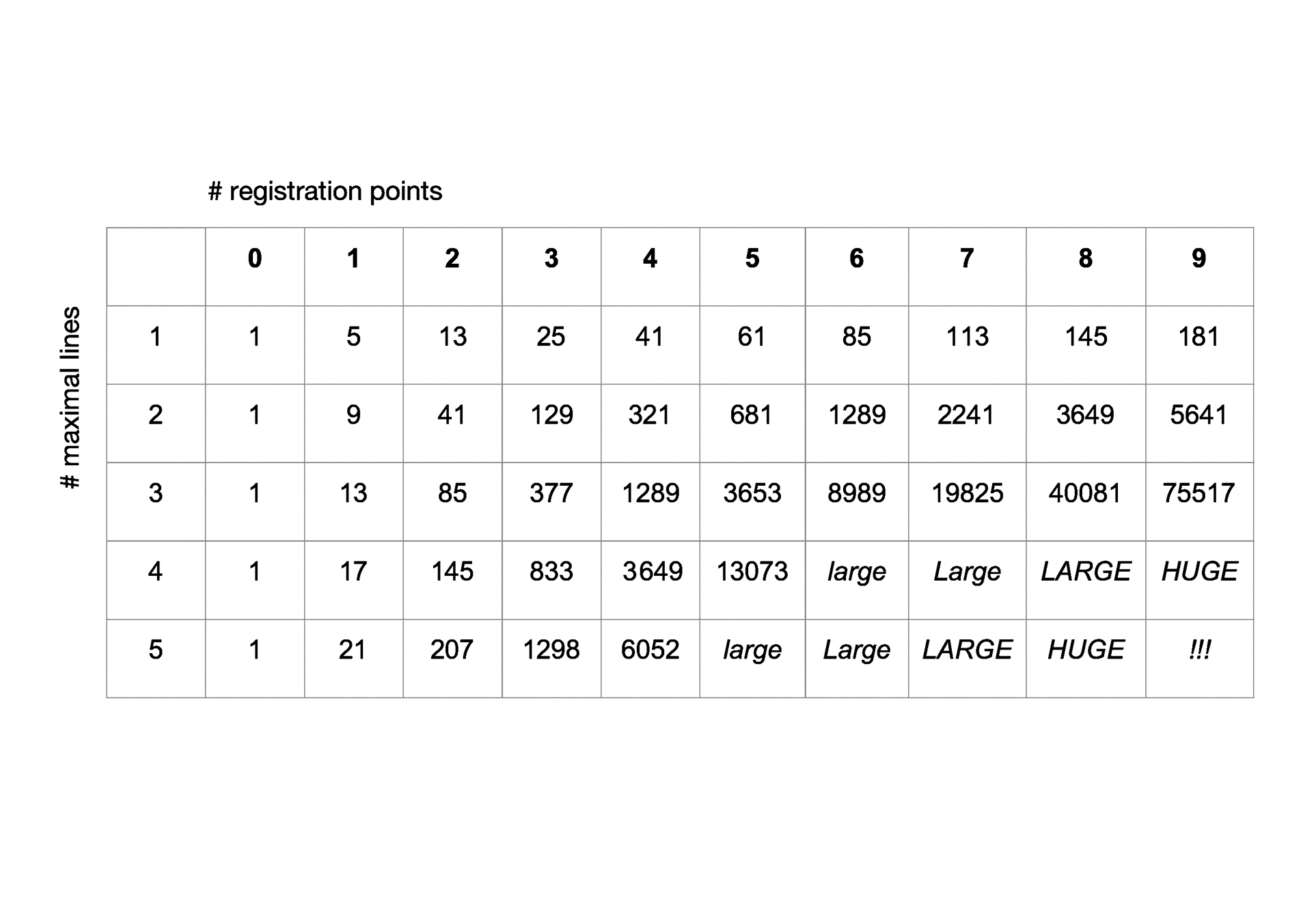
08. The number of ways to place n maximal lines on a construction line with k registration points is given by the sequences of 2n dimensional orthoplex numbers.
|
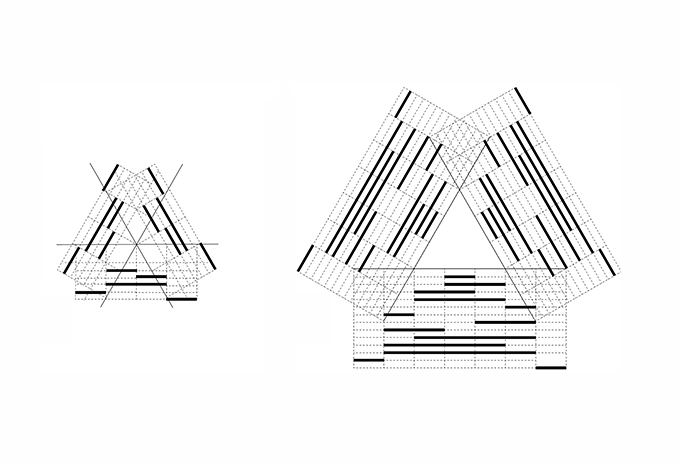
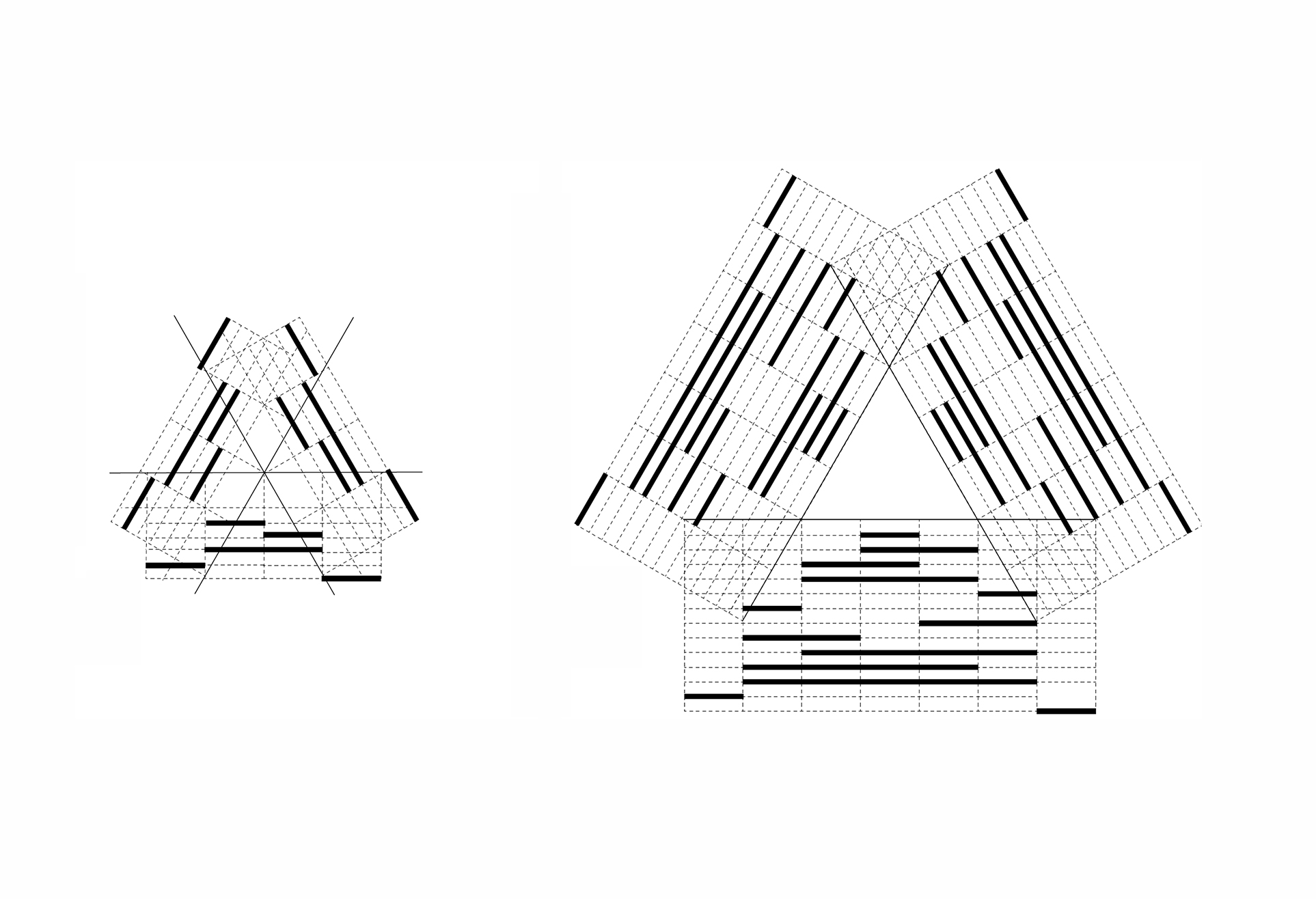
09. Counting shapes: Enumerate all maximal lines on each arrangement of construction lines. There are 125 shapes for the star-configuration. There are 2197 shapes in a triangular configuration.
|
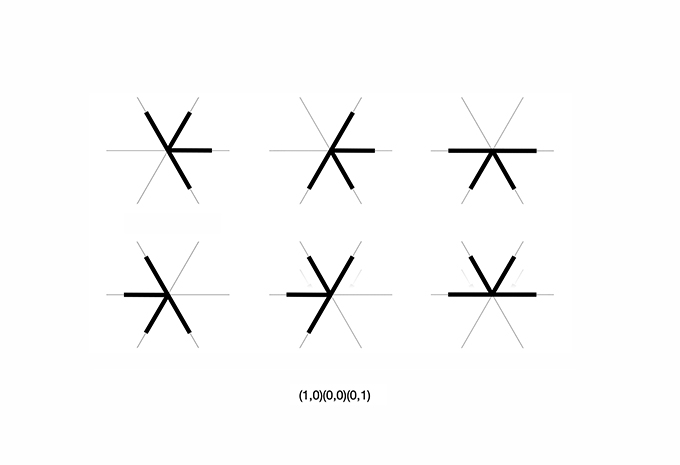
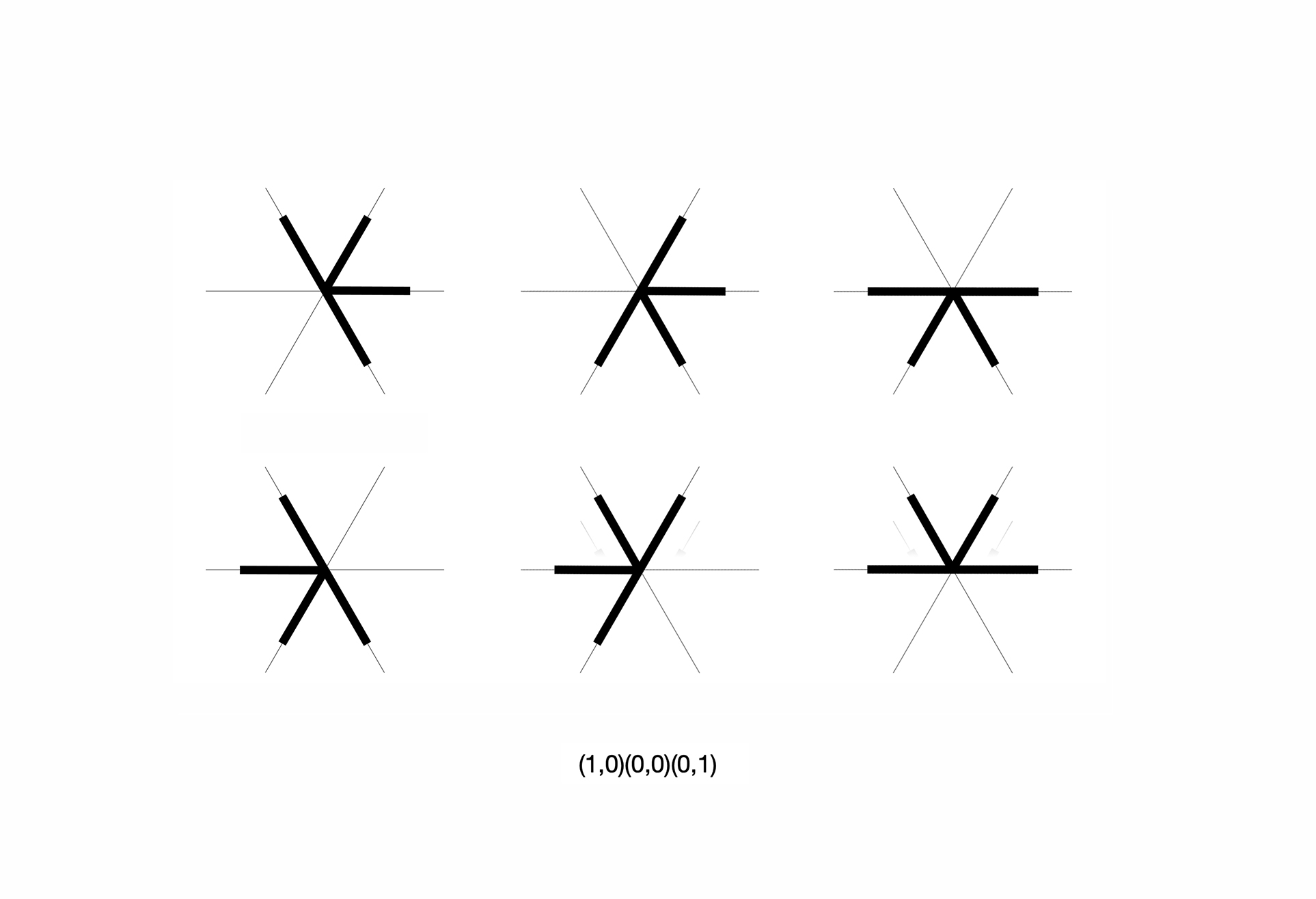
10. Counting non-equivalent shapes given a configuration of construction lines using groups of symmetries, Burnside’s lemma and Polya’s theorem of enumeration. Six symmetrical copies of the same shape.
|


11. Partially ordered set of the 19 distinct shapes on a 3-star arrangement after symmetry
|
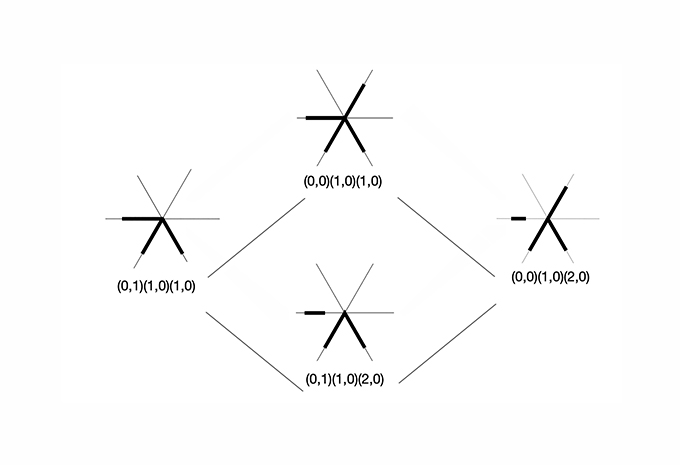
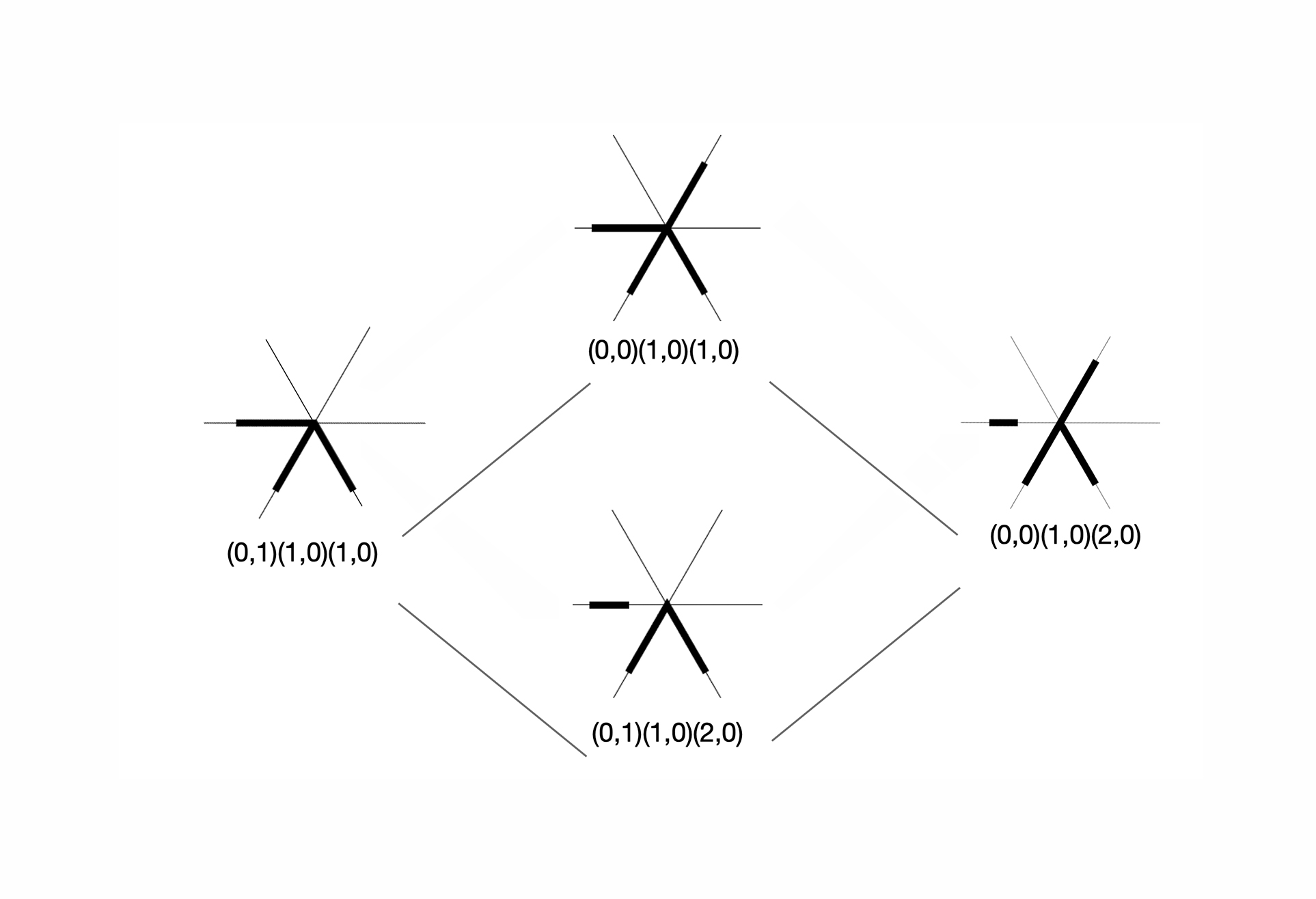
12. Encoding information with the shape signature
|


13. Some shapes consisting of 4 lines – among the possible 317,065 4-line shapes
|


14. Some shapes consisting of 4 lines - among the possible 317,065 4-line shapes
|
|
Shape Signature provides a new and uniform specification of parametric shapes consisting of points, lines, planes and solids. The model extends the shape grammar definition of a shape consisting of maximal elements of lines, planes and solids to the specification of parametric shapes consisting of maximal elements of lines, planes and solids to ultimately ensure that a specification of a parametric shape is unique - and even more, captured by a numerical formula. The method proceeds from considering a shape consisting of a collection of maximal lines upon an arrangement of hyperplanes to calculate and visually represent any parametric shape consisting of lines in CAD parametric models.
A key idea in the shape signature is the indefinite number of parts in a maximal element. This number is only defined with respect to the context where a maximal element is. For example, a line when it is in no spatial relation with some other line, it has 1 unlimited number of parts; the same line may have up to 5 parts when it is in a spatial relation with another line; 13 parts with 2 lines; 41 parts with 4 lines; and so forth, following the sequence of centered square figurate numbers and their corresponding powers in higher dimensions for more elaborate combinations of number of parts per line.
The very same parts combine one with another to create a visually staggering world rising from the singularity of the 1-line shape, to the 8 2-line shapes, to the 519 3-line shapes (among which there is the triangle and its parametric variations) and to the 317,065 4-line shapes (among which there is the square and its parametric variations). Checking these numbers, it is easy to see that any parametric shape consisting of 4 lines or strokes in the plane is an instance of the 317.593 possible 4-line shapes. The numbers for larger sets of lines increase dramatically to further the key insight of the formalism on a unique description of any shape out there.
The algebraic calculations of figure inventories for up to 4-lines so far are done in Mathematica. The calculation of the chirotopes for the underlying matroids are done by hand. The specification of the shapes is modeled in Grasshopper and visualized in Rhino. The project has been carried through with substantial help from Cvetelina Hill, May Cai and Nicholas Liao, doctorate and undergraduate students, respectively, at the School of Mathematics, College of Sciences at Georgia Tech.
|
|
|
|